2025.12.05

• システム運用
• 金融向けサービス
• その他
• 金融業
• 業務効率化

三菱総研ＤＣＳは、長年にわたり、金融システムの開発に取り組んできました。金融関連ソリューションの中でも、金融リスクの予測に要する計算量は膨大で、非常に多くの計算時間を要します。夕方から夜通しプログラムを動かし、翌日ようやく結果を得るといった状況も珍しくありません。そのため、お客様に情報を提供するまでにかかる時間の短縮が大きな課題となっています。

D-Wave社のクラウドサービス「Leap」では、量子処理ユニット（QPU）とハイブリッドソルバーが提供されており、解く問題の性質に応じてそれぞれソルバー*を選択することが可能である。「＊最適化問題など、特定の計算問題を解くためのアルゴリズムやソフトウェアのこと」
量子処理ユニット（QPU）とは、いわゆる量子アニーリングを用いたソルバーであり、ハイブリッドソルバーは量子アニーリングと古典コンピュータの組み合わせ型のソルバーである。

私たちは、量子アニーリングにアクセスできるようなアプリケーションを作成するにあたり、ライブラリとしてD-Wave Ocean SDKを利用した。
D-Wave Ocean SDKとは、Pythonプログラムを使ってD-Wave社のソルバーにアクセスして、問題を解くことを可能にするソフトウェアライブラリ群である。

例えばソルバーを使って問題を解くためのツールとして、はサンプラー（Sampler）が提供されている。これは同じ問題を複数回解くことで得られる解のサンプル集合を得るためのプロセスである。
最適化問題はQubo（Quadratic Unconstrained Binary Optimization：二次制約なし二値最適化）をもとに拡張されたBQMやCQMというモデルに変換して解くが、それぞれのモデルに応じてサンプラーが用意されている。
また、Leapには様々なデータを確認できるダッシュボードが用意されており、ダッシュボードにてソルバーごとの利用時間やジョブごとの実行時間や結果を確認した。

アニーリング方式の適用例として、まずは「ナップサック問題」について取り扱う。
問題設定は以下の通り。

”ある探検家がある洞窟を探検していました。しばらく洞窟の中を歩いていると、思いがけなく複数の宝物を発見しました。”

”しかし探検家の手持ちの荷物の中で宝物を運べるような袋としては、残念ながら小さなナップサックしか持ち合わせていませんでした。 ”
”このナップサックには2kgの荷物しか入れることができません。”
”探検家はこのナップサックに入れる宝物の価値をできるだけ高くしたいのですが、どの荷物を選べば最も効率的に宝物を持って帰ることができるでしょうか。”

出典： OpenJij : Ising model と QUBOのためのヒューリスティクスソルバー

※外部サイトに遷移します

上記の問題をBQMのソルバーで計算する。
BQMで計算する場合、QUBOのエネルギー関数の形に式を変換する必要がある。
まずは問題の定式化を行う。

・定式化
　今回の問題設定を定式化すると以下のようになる。
　＜目的関数＞

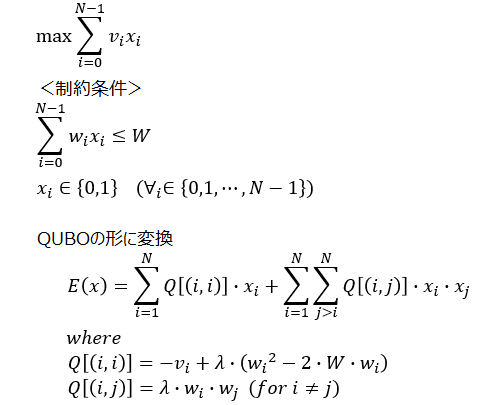
・プログラミング
上記の定式化は以下のようにプログラムできる。

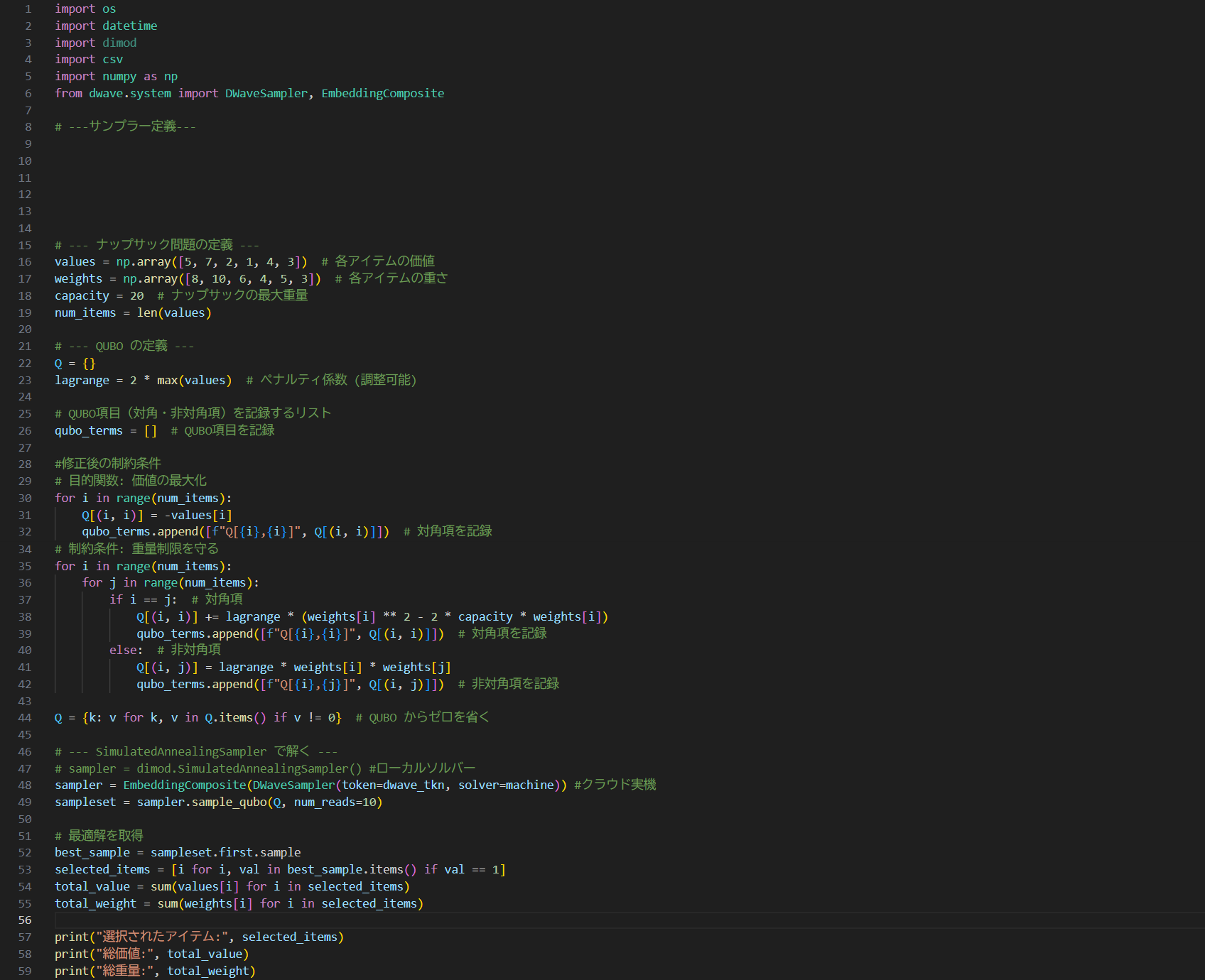
ポイントとなるのは下記の部分

BQMでは、目的関数内に制約条件を組み込み、「ペナルティ」という形で表現する
式全体としてはエネルギー関数が小さくなることを期待しているため、ペナルティは制約条件に違反するとエネルギー関数を大きくするようになっている。
したがって、適切な解を得るためにλ(Lagrange)およびペナルティの式を調整する必要がある。

・計算結果
選択されたアイテム: [1, 2, 3]
総価値: 10
総重量: 20

現状は以下の通り読み取り回数を10回としている。これを100回に増やすと結果は

選択されたアイテム: [0, 3, 4, 5]
総価値: 13
総重量: 20

となり、より最適な解が採択されるようになる⇒精度が上がる

同じ問題をCQMのソルバーで計算する。
CQMの場合は、制約条件を目的関数内に取り込むことなく、制約条件として扱うことが可能。

・定式化
定式化については先ほどと同様

・プログラム

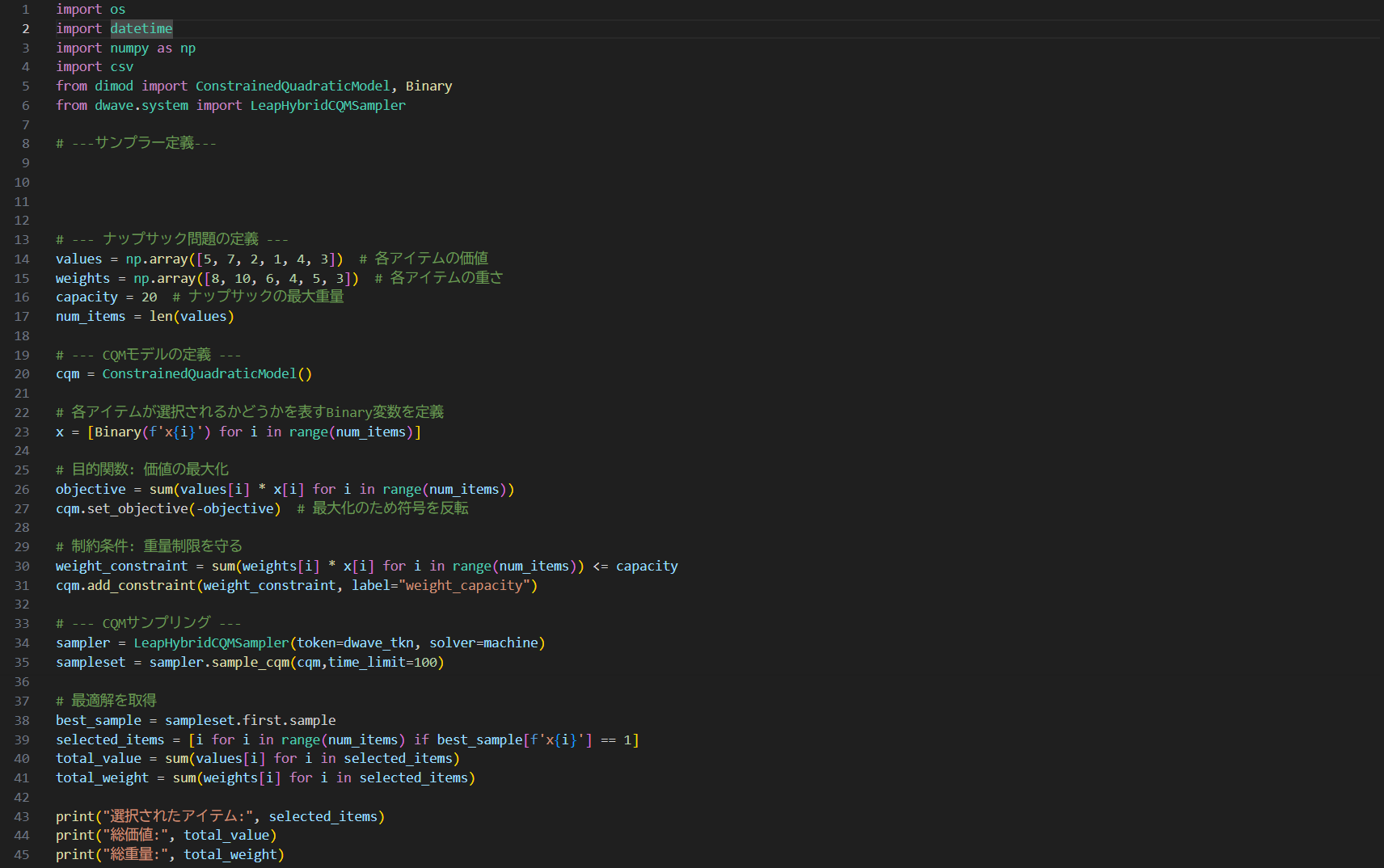
ポイントとなるのは下記の部分

CQMでは、以下の制約条件を直接的に扱うことができる。
＜制約条件＞

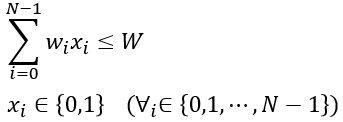
・計算結果
選択されたアイテム: [0, 1, 5]
総価値: 15
総重量: 21

CQMでは読み取り回数ではなく、1つの問題に対する探索時間を設定する。（デフォルトは5秒）

元のプログラムの指定は10秒であり、10秒の間に制約を満たす最適解が発見できなかった状態。
なお、それ以外のオプションは指定できない。

これを100秒に増やすと
選択されたアイテム: [1, 4, 5]
総価値: 14
総重量: 18

となり、より最適な解が採択されるようになる。⇒精度が上がる

『ポートフォリオ最適化入門』（枇々木規雄　2016）における、「平均・CVaR モデル」を前提とする。
資産投資によって資金を増やしたいとき、その運用結果を測る尺度は収益率である。
銀行預金の場合は金利が収益率にあたる。

一方、株式の場合は将来の収益が確定していないため、収益率は不確実である。
このようなリスク資産に投資を行う場合、ポートフォリオを組み複数資産に分散投資を行うことでリスクを低減させる。
その理由は単一資産に全資金を投資すると、大きな損失を被るためである。
複数資産に分散投資した場合は、ある資産分の損失を他資産でカバーできる可能性がある。
分散投資した全資産で損失を被る可能性も当然あるが、その確率は単一資産の損失可能性よりは小さくなる。

資産投資を行う場合、高収益・低リスクを求めたいが、一般的に両者はトレードオフの関係にある。
上記を勘案して最適なポートフォリオを選択するために数理計画モデル（＝ポートフォリオ最適化モデル）を用いる。

VaRは確率水準を明示的にパラメータとして用いたわかりやすいリスク尺度で、金融機関のリスク管理に用いられている。
VaRは確率水準β（例：β=0.95）で発生する最大損失αβを表している。⇒95%の確率で損失はα以下になる。
VaRは損失の大きさを表すため、収益率として記述する際はマイナスを付与する。

しかし、VaRはその値を上回る大きな損失と小さな損失を区別できないため、直接的にVaRを上回る損失の分布を評価できない。
これはリーマンショック後の株式市場のように極端な株価の下落を評価する場合に大きな欠点となる。
VaRと同様に確率水準を明示的に取り扱いつつ、VaRを上回る損失も評価できる尺度としてCVaRを用いることができる。
バーゼルⅢでも期待ショートフォール(ES：Expected ShortFall、CVaRの別称)に基づき自己資本を計算することが提案されている。
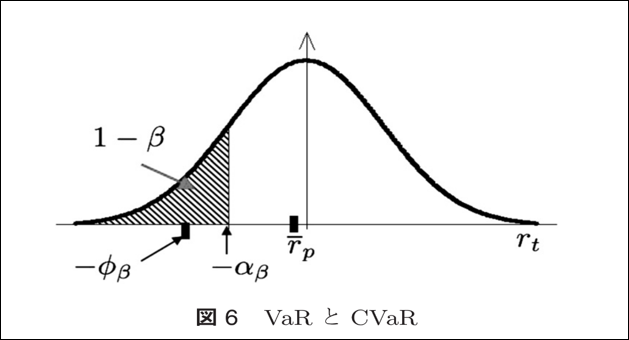
CVaRはポートフォリオ収益率の損失がαβ（VaR）を上回る場合の損失の条件付期待値を表し、以下で定義される。

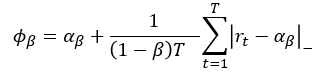
横軸を収益率としてVaR、CVaRの例を以下に示す。

・定式化
『ポートフォリオ最適化入門』（枇々木規雄　2016）における、「平均・CVaR モデル」を前提とする。
CVaRはポートフォリオ収益率の損失がαβ（VaR：Value at Risk）を上回る場合の損失の条件付期待値を表し、以下で定義される。

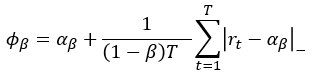
計画問題の文脈では以下のような最小化で表現される。
＜目的関数＞

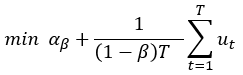
＜制約条件＞

今回の例では、資産数6、シナリオ数250にてポートフォリオ最適化を行う。
使用したデータは

収益率

・プログラミング
上記の定式化は以下のようにプログラムできる。

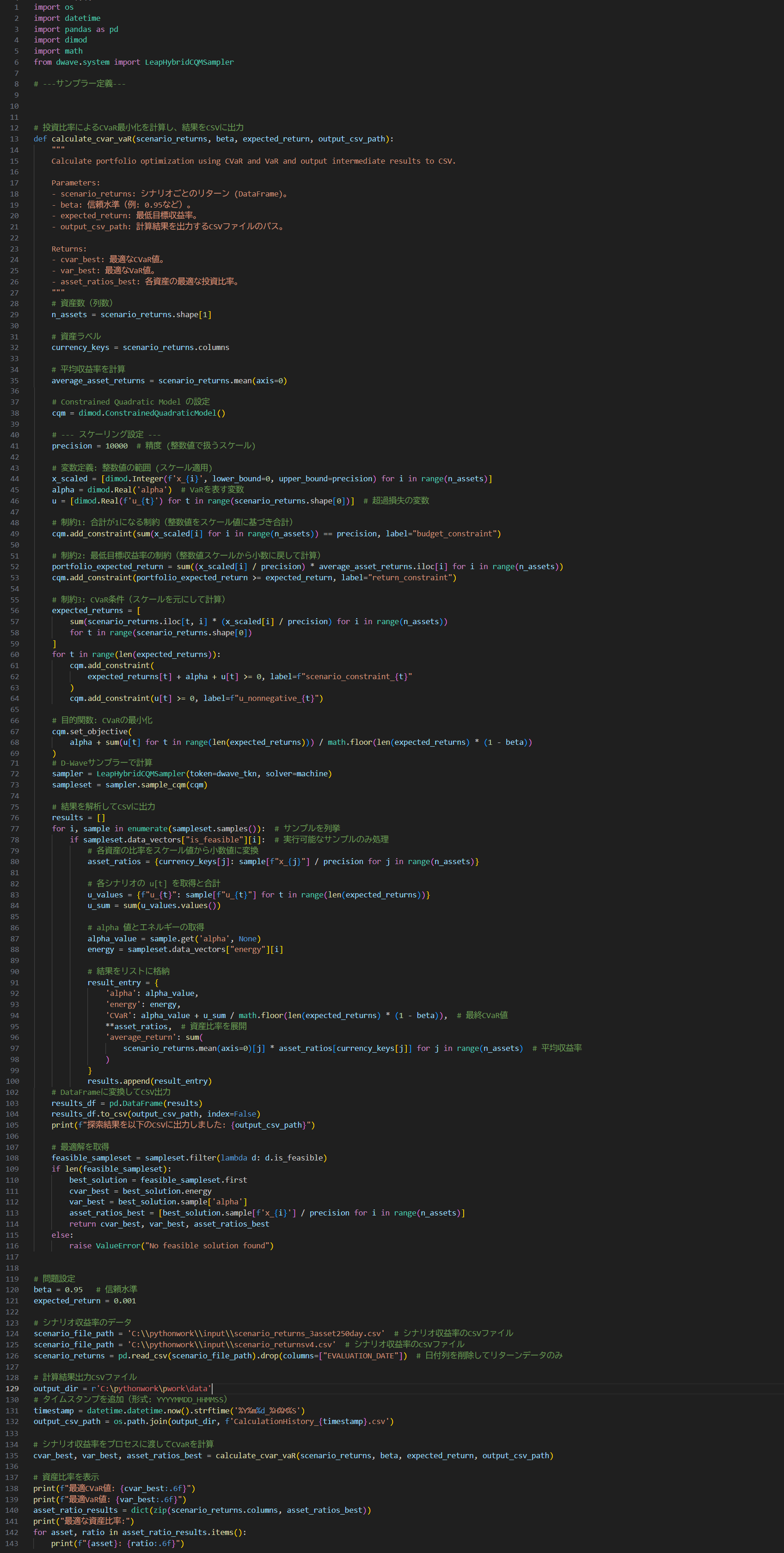
ポイントとなるのは下記

そのまま投資比率を扱うと小数桁が増えすぎて探索範囲が膨大になってしまう。
そのため、スケーリングによって小数桁数を制限している。
今回であれば小数4桁まで。

・計算結果
最適CVaR値: 0.042125
最適VaR値: 0.035355
最適な資産比率:
A: 0.339700
B: 0.019400
C: 0.259300
D: 0.126000
E: 0.221800
F: 0.033800

本研究では、量子アニーリング方式の基本的な動作原理を理解し、ポートフォリオ最適化問題をテーマに Python を用いたプログラム実装と、実機による動作確認を行った。
このことにより、量子アニーリング方式の理論と実装を一気通貫で把握することができた。

実機を用いた検証では、D-Wave社のクラウドサービス「D-Wave Leap」にて、Ocean SDK を用いたプログラミングを実施した。
D-Wave社の提供する Hybrid Solver を用い、ポートフォリオ最適化問題について求解可能であることが確認できた。

今後も量子アニーリング方式の最新動向を注視していきたい。